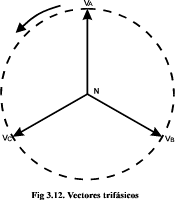
Un sistema de formas de onda senoidales trifásicas puede ser representado mediante tres vectores rotatorios (fasores). La velocidad de rotación (rev/s) informa sobre la frecuencia, la posición instantánea informa acerca del estado dentro de un ciclo y la longitud del vector representa la amplitud de la tensión o de la corriente que están siendo representadas (figura 3.12). La tensión simple (fase-neutro) queda representada por las longitudes de VA-N, VB-N, VC-N, en tanto que la tensión compuesta viene dada por la longitud de los segmentos VA-VB, VB-VC, VC-VA.

En un puente inversor trifásico, intentamos reconstruir señales senoidales, pero no podemos conseguir una forma de onda perfectamente senoidal dado que no tenemos la capacidad de mantener la rotación de forma continua.

Existen ocho posibles estados de las salidas A, B y C, dependiendo de los IGBT que conduzcan. Dos de esos estados corresponden a un valor nulo de la tensión, en tanto que los otros seis corresponden a seis puntos espaciados 60º entre sí. En la figura 2.13 aparece una tabla que refleja esos ocho estados, así como el estado de los interruptores. Moviéndonos de forma secuencial entre estos seis estados activos podemos generar en la salida una onda semi-cuadrada, como se indica en la figura 3.8.

            Clave: 0 = transistor OFF                  + = salida +Ve

                        1 = transistor ON                    - = salida -Ve

                                                                        0 = salida 0 voltios

Los ocho estados de la tabla pueden ser representados mediante una estructura hexagonal, como se muestra en la figura 3.14. Es de remarcar que el paso de un estado al adyacente, o de un estado activo al nulo, únicamente requiere cambiar el estado de dos IGBT. Este hecho es de gran importancia para lograr la mayor frecuencia de conmutación posible con un número mínimo de interruptores, a fín de minimizar las pérdidas por conmutación.

Para generar un vector tensión intermedio, esto es, un vector cuya magnitud y desfase no se corresponda con una de las seis esquinas del hexágono, es necesario modular entre dos estados activos adyacentes (para fijar el desfase) y uno de los estados nulos (para fijar la amplitud), tal como se muestra en la figura 3.15.

Las ventajas de la modulación del espacio vectorial sobre la modulación sinusoidal son las siguientes:

Reducido contenido de armónicos en el motor. Esto repercute en una reducción de las pérdidas. La razón estriba en que la frecuencia de conmutación efectiva es mayor que en la modulación sinusoidal, para una frecuencia de conmutación determinada.

Pequeños pares pulsatorios. Los pares pulsatorios producidos por las variaciones del flujo magnético en el entrehierro del motor son menores cuando se utiliza la modulación del espacio vectorial. Estas pulsaciones se producen a la frecuencia de modulación, produciendo un ruido audible (de origen magnetoestrictivo) en el motor.

Frecuencia de modulación constante. La modulación sinusoidal es síncrona, esto es, la frecuencia de modulación se ajusta al fundamental de la frecuencia de salida del inversor. La modulación del espacio vectorial es asíncrona, lo que significa que la frecuencia de modulación (y en consecuencia la frecuencia del ruido del motor) es constante en todo el rango de frecuencias.

Mejor uso de la tensión de alimentación. En la modulación sinusoidal, si accidentalmente la amplitud de la referencia supera la señal portadora (figura 2.10), puede producirse la saturación de la modulación con el consiguiente incremento de la distorsión en la forma de onda de la tensión. Llevado al extremo, el resultado serían ondas semi-cuadradas. Con la modulación del espacio vectorial, los límites máximos de la tensión de salida sin distorsión vienen determinados por un círculo inscrito en el hexágono, como muestra la figura 3.16. La máxima tensión sin distorsión es el 115% de la que se puede lograr con moduladores sinusoidales, lo que conlleva un mejor uso de la tensión disponible en el bus de continua. Sin embargo, a partir de este nivel, las formas de onda de salida pasan a ser trapezoidales.

Adaptada a la generación de formas de onda mediante microprocesador. Las técnicas de modulación del espacio vectorial sólo son realizables en sistemas digitales basados en microprocesador. Es posible variar la frecuencia de modulación para adaptarse a las características de los IGBT, o utilizar diferentes frecuencias de modulación para reducir el ruido aparente del motor, como hace la modulación "Whisperwave" de PDL.

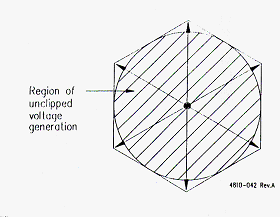
Figura 3.16: Límites de la tensión de salida

Información facilitada por el departamento técnico de: